Solitons

Les solitons sont un type d'ondes qui apparaissent souvent des équations de propagation non-linéaires et autres phénomènes de fluides. De telles ondes se propagent dans leur milieu sans se déformer, et on peut en modéliser plusieurs de telles sortes que deux solitons rentrent en contact et "fusionnent" en un soliton plus grand pendant un certain temps.

Voir ici et là.

Etant donné quelques solutions analytiques à l'équation non-linéaire de KdV on peut modéliser la propagation de quelques solitons en deux dimensions avec OpenGL :

On obtient également des phénomènes de propagation analogues en 3D, avec ici un soliton isolé :

Ou encore 2 solitons en interaction :

Diffusion de matière

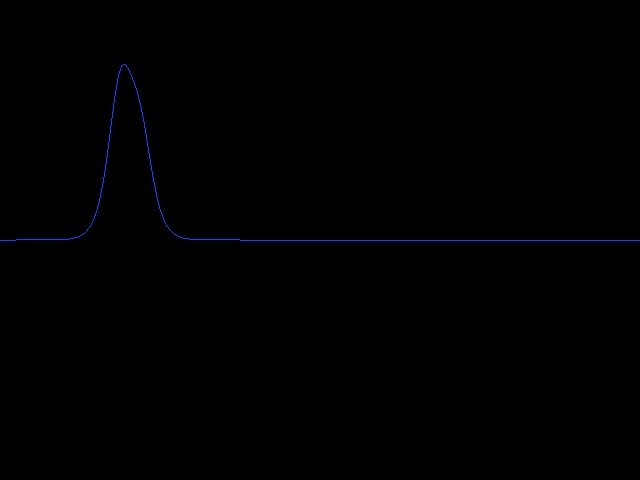
Soit l'équation de la chaleur à une dimension :

Qui se généralise sans aucun problème avec un laplacien à plusieurs dimensions, et où on néglige le coefficient de diffusion qu'on pose à 1.

Pour la résoudre numériquement sur une grille 2D, on divise le plan en petites cases (N*N), on a un tableau de deux (ou une seule avec un petit calcul) dimensions qui correspondra à la quantité u qui sera diffusée. L'évolution de u sera simplement :

u[i][j] += K*(u[i+1][j] + u[i-1][j] + u[i][j+1] + u[i][j-1] - 4*u[i][j])*4*N

L'implémentation de cette version très simplifiée d'une diffusion donne des résultats assez convaincants, par exemple cette diffusion correspond à la donnée initiale de trois points centraux de densité : 

Voici le résultats obtenu avec comme configuration initiale une barre très dense :